물체를 모델링할 때 고려할 특성은 크게 3가지가 있다.
1. Geometric property (기하학적 특성)
2. Material property (텍스처, 색상 등)
3. Behavior property (애니메이션과 같은 동작)
텍스처와 색상은 다음 글에서 더 자세히 보고, 이번 글에서는 기하학적 특성을 중점적으로 정리한다.
Geometric Model
기하학적 모델을 만드는 방법은 크게 3가지가 있다.
1. 손수 그리기
공간 크기를 직접 계산해서 그리거나, 모델링 툴을 활용해서 직접 조각하여 만들 수 있다.
2. 알고리즘 (Algorithmically)
3. 스캐닝
기하학적 모델을 표현하는 방식은 크게 4가지가 있다.
1. Raw Data
2. Surface (표면만 모델링)
3. Solid (내부까지 모델링)
4. High-level Structure
Raw Data
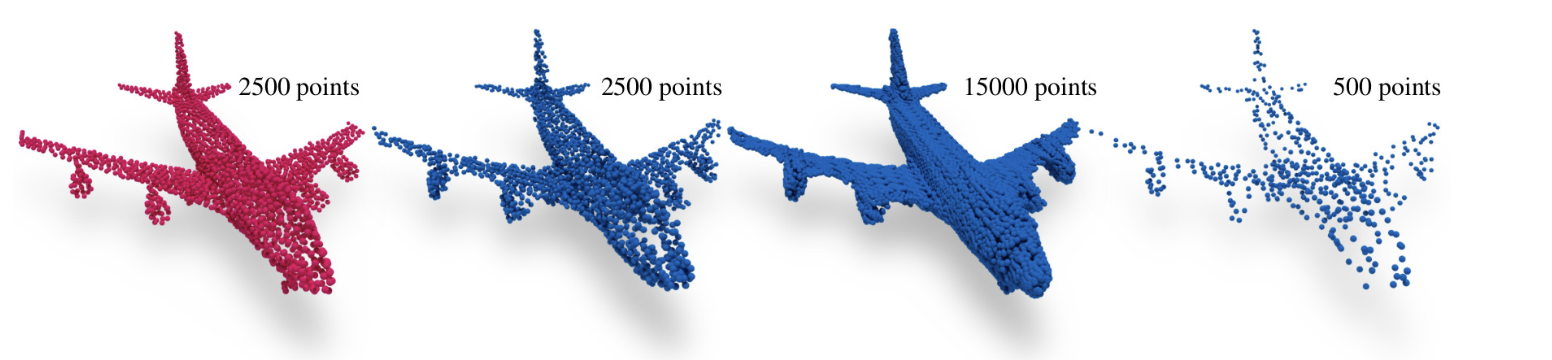
3차원 점들의 집합으로 모델링하는 방식이다.
이 점들의 집합을 가리켜 point cloud 라고 말한다.
각 점들 사이의 관계를 고려하지 않고, 점 데이터 그 자체를 여러개 모아서 모델링하는 간단한 방식이다.
사용되는 점의 개수에 따라 표현의 정확도가 달라진다.
Surface
점들 사이의 관계를 이용해서 물체의 겉표면을 모델링하는 방식이다.
이 경우, 점 사이의 관계를 기술해서 물체의 부드러운 곡면을 표현하는 것이며,
표면에는 어떤 구멍이나 흠집없이 매끄러운 곡면이 만들어져야 한다. ( = manifold 를 이루어야 한다)
표면을 모델링하는 방법은 크게 3가지가 있다.
1. polygon mesh : 물체의 표면을 다각형으로 쪼개서 표현하는 방식
2. parametric surface : 수학적으로 표현하는 방식 (매개변수 곡면)
3. implicit surface : 수학적으로 표현하는 방식 (함축적 곡면)
Polygon Mesh

삼각형 또는 사각형을 사용하여 표면을 표현하는 방식이다.
mesh polygon 또는 polygon mesh 라고 부르며, 대부분의 3D 모델링은 이 방식을 사용한다.
mesh 는 물체의 표면을 정의하는 꼭짓점, 변, 면의 집합을 말한다.

이 그림에서 보는 것처럼 직육면체를 표현하기 위해 10개의 점을 먼저 정의하면
이 점들을 연결한 선분이 나오고, 이 선분이 모인 단위면(face)이 나오고
단위면이 모여 polygon 을 이루면 (같은 면을 구성하는 face 집합) 이들이 모여 surface 를 구성하게 된다.
Mesh 는 이해하기 쉬우며 다루기 간단하고 대부분의 경우 효율적이라는 장점이 있다.
간단한 물체, 복잡한 물체 모두 적용이 가능하고 (versatile)
물체의 크기에 상관없이 적용할 수 있다. (scalable)
하지만 머리카락, 액체와 같이 곡면이 많고 굴곡이 심한 물체를 모델링하는데는 적합하지 않다는 단점이 있다.
(표현할 수는 있으나 데이터가 많이 필요해서 효율적이지 않다)
Parametric Surface
이렇게 굴곡이 심하고 곡면이 많은 물체를 모델링할 대는 수학적인 방법을 사용하는 것이 더 좋다.
parametric surface 는 유클리드 공간에서의 평면을 말한다.
즉, 2개 파라미터를 가진 R2 평면으로 3개 파라미터를 가진 R3 를 표현하는 방법이다.
간단한 수식으로는 아래와 같이 나타낼 수 있다.

3차원 점을 표현하려면 (x, y, z) 3개의 점이 필요하다.
이때 z 의 값을 f(x, y) 로 정의하여 (x, y) 라는 2개의 정보만으로 3차원 공간을 표현하는 것이 parametric surface 이다.
이 방법은 f(x, y) 를 잘 정의하는 것이 중요할 것이다.
또한 parametric representation 에는 크게 Patch, Control points 2가지 방법이 있다.
Parametric Surface 를 사용하여 곡면을 표현하는 방법에는 여러가지가 있지만
그 중에서 Bezier Curve 방식과 B-Spline 방법에 대해 정리해본다.
- Bezier Curve
p0 부터 pn 까지 control point 의 집합으로 정의되는 곡선이다.
이때 n 은 curve 의 차원을 이야기하며,
n = 1 이면 1차원 (linear = 선형함수)
n = 2 이면 2차원 (quadratic = 2차함수)
n = 3 이면 3차원 (cubic = 3차함수)
...
으로 뻗어나가는 식이다.
또한 첫 번째와 마지막 control point 는 곡선의 양 끝점으로서 항상 고정되어있다.
하지만 그 사이에 있는 control point 들은 보통 곡선 위에 존재하지 않는다.
- n = 1 인 경우 (linear bezier curve)

p0, p1 2개의 점 사이에 곡선이 있으며, 그 사이의 점들은 t 라는 매개변수를 통해 표현한다.
t = 0일 때는 p0 을 가리키고, t 값이 점점 증가하여 1에 가까워질수록 P1 을 향하게 된다.
이 t 값에 따라서 점이 그리는 경로가 우리가 그릴 곡선이 된다.
(사실상 우리가 평소에 알고있는 직선식이다)
- n = 2 인 경우 (quadratic bezier curve)

n = 1 과 비슷하지만, 기준점이 p0, p1, p2 로 3개이다.
p0, p1 2개 점으로 만들어진 선 위의 점과,
p1, p2 2개 점으로 만들어진 선 위의 점 2개를 통해 곡선을 표현한다.

위키피디아 그림을 빌리면 시각적으로는 이렇게 표현된다.
p0, p1, p2 로 두 직선을 어떻게 정의하는지에 따라 그 사이에 그려지는 곡선의 형태가 바뀐다.
p0, p2 는 곡선의 양 끝점, p1 은 곡선 밖에 있는 점 (위 그림에서 x 로 표시된 점) 이다.
p1 은 이 곡선의 형태를 결정하는데 사용되는 control point 이다.
p1 이 control point 이기 때문에 위 수식을 P1 기준으로 풀어보면

이렇게 정리할 수 있다.
이 식을 t에 대해 미분해보면 이 곡선의 기울기 변화를 알 수 있다.
점은 P0 에서 시작하여 P1 방향으로 가다가, P1 방향에서 P2 방향으로 틀어서 이동하는 형태를 띄는 것을 알 수 있다.
- n = 3 인 경우 (cubic bezier curve)
마지막으로 n = 3 인 경우에는 P0, P1, P2, P3 4개 점으로 곡선을 표현한다.
이때 P0, P3 은 곡선의 양 끝점이 되고 P1, P2 는 control point 로서 곡선의 형태를 결정한다.

그림으로 3가지 경우를 정리해보면 위와 같다.
n = 1 일 때는 컨트롤 포인트가 없이 직선이 나오고 (양 끝점도 control point 라고 하지 않았나?)
n = 2 일 때는 1개의 control point 로 직선을 만들고
n = 3 일 때는 2개의 control point 로 직선의 형태를 결정한다.
즉, n 값이 커질수록 control point 개수가 늘어나면서 더 복잡한 곡선을 표현할 수 있게 된다.
- B-Spline
B-Spline 은 n차원의 조각 다항식 (piecewise polynomial) 으로 곡면을 나타내는 것을 말한다.
즉, 각 점마다 끊어서 여러개의 수식을 통해 곡선을 표현하는 것이다.
(함수를 정의할 때 구간을 나눠서 각 구간별로 다른 다항식으로 함수를 정의한 것)
보통 cubic B-Spline 또는 NURBS(Non-uniform rational B-Spline) 같은 방법을 사용한다.
NURBS 는 유리수를 사용하여 베이저 커브와 B-Spline 을 일반화한 방법이다.
B-Spline 은 모서리가 없이 곡면으로 이루어진 surface 를 정확하게 표현한다는 특징이 있다.
Implicit Surface
함축적 곡면은 말 그대로 implicit 함수를 사용하여 곡면을 표현하는 방법이다.
3차원 공간 상의 점 P 에 대해, 3차원을 1차원으로 변환하는 함수 f 를 정의하고
f(P) = 0 을 만족하는 모든 P 가 모여 곡면을 구성한다고 표현하는 것이다.
즉, f(x, y, z) 로 3개의 파라미터를 통해서 정의되는 함수에 대해
이 함수의 값이 0이 되는 점들의 집합으로 표면을 표현하는 것이 implicit surface 이다.

예를 들어 평면과 구는 이런 수식으로 표현할 수 있고
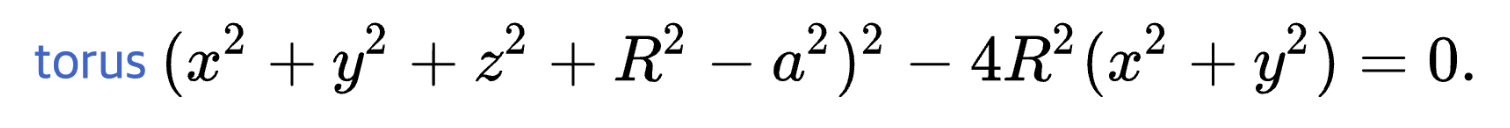
도넛 모양 곡면은 이렇게 표현할 수 있다. (R, a 값은 그 크기와 형태를 결정하는 상수값)

예를 들면 이런 식으로 그려진다.
이 방식에 속하는 다른 표현 방법으로는 SDF (signed distance field) 방식도 있다.

이 방식은 p1, p2, p3, p4 4개의 점을 뽑은 뒤,
이 4개의 점 사이의 거리를 구해서 위 수식에 넣은 결과 값이 똑같이 나오는 모든 점 p 를 가지고 곡면을 표현하는 것이다.

그러면 이런 식으로 그려진다고 한다.
implicit surface 로 표면을 표현하는 다른 방법으로 그래프를 회전시켜서 표면을 계산하는 방법인 surface resolution 이 있다.
예를 들어 z = f(x) 라는 그래프를 두고, 이 그래프를 z 축에 대해 회전시켜서 표면을 얻는 방식이다.

회전의 정도, 그래프 정의를 모두 포함하면 위와 같이 함수를 정의할 수 있다.

이 식의 결과로 이런 와인잔 모양의 표면을 얻을 수 있다.
이렇게 parametric surface, implicit surface 방식으로 곡면을 표현하면
보다 적은 데이터(파라미터 개수에 의존)로 세분화된 모델링을 할 수 있으며, interfacitve 하다는 장점이 있다.
하지만 곡면을 계산하는데 많은 시간이 걸린다는 큰 단점이 있다.
그래서 이 방식으로 먼저 식을 세운 다음, 특정 위치의 점만 콕콕 찝어 계산한 뒤, 그 점을 기반으로 mesh 방식을 사용하여 렌더링하는 방법을 많이 사용한다.
High-Level Structure
모델링을 할 때 물체의 생성과 같은 '과정' 까지 포함된 경우에 사용하는 방법이다.
즉, 코딩을 통해서만 모델링할 수 있는 경우를 말한다.
대표적으로 Procedural Model, Particle System 이 있다.
- Procedural Model
시간에 따라 변할 수 있는 규칙 집합을 기반으로 3D 모델 또는 텍스처를 생성하는 것
즉, 물체의 생성 과정이 모델링에 포함되는 경우를 말한다.
대표적인 예시로 Fractal, L-system, CSG 가 있다.
- Fractal
자신의 형태가 부분적으로 계속 반복되는 것 (recursive)
이런 형태를 모델링하려면 재귀함수 호출하듯 반복되는 동작을 계속해서 동적으로 생성해야 한다.
이런 Fractal 을 '자기유사 Fractal' 이라고 하며, Koch curve, Binary split tree 와 같은 것이 있다.
복소수를 이용해서 점화식 기반으로 프랙탈을 정의하기도 한다. (불변 Fractal)

점화식은 이런 형태로 작성되며, C 값이 변화함에 따라 Z 가 증가하기도 하고, 왕복하기도 한다.
Z 가 무한히 발산하지 않는 각각의 C 값을 화면위에 점으로 표현하면 프랙탈이 그려진다.
이런 프랙탈 기법은 산, 나무와 같은 자연물을 모델링할 때 자주 활용된다.
- L-system (Lindenmayer system)
프랙탈과 비슷하지만, 일종의 formal grammar (문법) 을 통해 모델링하는 방식이다.
컴포넌트는 알파벳(심볼), production rule, 초기 string (axiom) 으로 구성되어 있고
이 초기 문자열로부터 생성되는 문자열을 기하학적 구조로 변환하는 메커니즘도 컴포넌트에 들어있다.

문법 G 를 이렇게 정의할 때
V 는 알파벳, w 는 시작 문자열 (axiom), P 는 production rule set 을 가리킨다.
각각의 production 은 주어진 문자열과 그 문자열에서 넘어갈 다음 문자열로 구성된다.
- CSG (Constructive Solid Geometry)
속이 차있는 solid 를 만들어나가는 (constructive) 과정이 모델에 포함되어 있는 방법이다.
대부분의 CAD 프로그램에서 사용하며, basic primitive 와 boolean 연산자를 활용해서 만든다.
boolean 연산자에는 union, intersection, difference 와 같은 연산이 있다.
(집합 연산에 가깝다)

구와 직육면체(basic primitive) 2개 solid 에 대해 위에서부터 union, difference, intersection 연산을 적용한 결과를 보여준다.

기본 도형에서 시작해서 이 연산을 반복적으로 적용하면 위와 같이 복잡한 물체도 표현할 수 있다.
- Particle System
말 그대로 작은 입자를 모델링하는 것이다.
불, 물, 폭발과 같이 불규칙적이며, 역동적인 변화를 표현한다.
원시적인 입자를 활용하여 표현하며, 입자의 형태, 위치, 속도/가속도, 투명도 등이 시시각각 변화한다.
이런 변화들에는 랜덤성이 있기 때문에 확률적 특성이 들어가고
각 입자가 개별적으로 변화하기보다 군집적으로 변화하는 모양을 띈다.
파티클 시스템을 모델링할 때는 크게 3가지 stage 를 거쳐 모델링한다.
1. Emission Stage
첫 입자들이 만들어지는 단계,
각 입자들의 속도와 같은 속성을 결정하고, 각 입자들의 스폰 비율에 따라 단위 시간당 입자들이 만들어지는 속도가 결정된다.
2. Simulation Stage
새로운 파티클을 만들고, 기존 파티클의 속성(위치, 속도, 가속도 등)을 변화시킨다.
필요한 경우 충돌처리를 하기도 하며, 각 입자의 lifetime 에 따라 일정 시간이 지나면 사라지거나 변화하도록 만든다.
3. Rendering Stage
대부분 billboard quad 형태로 렌더링한다.
billboard 는 항상 관찰자를 향하는 평면을 말하고, quad 는 4개 꼭짓점으로 구성된 사각형을 말한다.
즉, billboard quad 는 입자를 표현할 때 항상 관찰자를 향하는 사각형 단면의 형태로 입자를 표현하는 것이다.
이 방법 말고도 하나의 픽셀 또는 단순한 3D 모델로 입자를 표현할 수도 있다.
다양한 모델링 방법들
지금까지 기하학적 모델을 만드는 방법을 살펴보았다.
이제는 그 외에 3D 물체를 모델링하는 다양한 방법들을 살펴보자.
Image-based Modeling / Rendering
2D 사진을 기반으로 3D 모델링하는 방법이다.
3D reconstruction 이라고도 한다.
Photogrammetry (사진계측), Disparity, 소실점 등을 활용하여 모델링 할 수 있다.
사진 계측은 사진을 기반으로 두 물체 사이의 거리를 재는 등, 물리적인 값을 측정하는 것이다.
disparity 는 두 눈에서 하나의 물체를 보는 각도가 미세하게 다른 것을 활용하여
두 눈 위치에 있는 2개의 카메라 각도 사진으로부터 3D 물체를 복원하는 기법이다.
이를 위해 첫 번째 사진에 있는 점이 두 번째 사진에서 어디에 있는지를 찾고 (correspondence problem)
이 두 점의 픽셀 차이를 이용하여 3차원 복원을 한다.
소실점 (물체의 원근감을 나타낼 때의 기준점) 을 활용하여 복원하는 방법의 경우, 상세한 복원이 어렵다는 단점이 있다.
Human Modeling
사람을 모델링하는 것은 앞서 정리한 모델링 기법만으로 하기 쉽지 않다.
특히 머리카락과 같은 털의 경우, 그 숫자가 매우 많기 때문에 하나하나 모델링하는 것이 어렵다.
사람 피부도 단순히 모델링한다고 사람 피부처럼 보이지 않는다.
빛의 반사가 겉에서 일어나는 경우, 조금 안에서 일어나는 경우 등 다양하기 때문이다.
또한 사람이 입고 있는 옷을 모델링하는 것도 쉽지 않다.
옷의 질감, 구겨짐과 같은 것도 다 모델링해야 하기 때문이다.
그래서 이런 모델링을 위해 Poser 와 같은 프로그램을 사용한다.
영화를 만들 때는 사람을 디지털화 시킨 virtual actor 를 사용할 수 있다.
Machine Learning
최근에는 기계학습을 이용하여 모델링을 할 수 있다.
Trellis 라는 모델은 이미지와 text 기반으로 3D 모델링을 만들어주며
사람 얼굴을 생성하는 모델, 애니메이션을 자동으로 생성하는 모델 등도 존재한다.
공간 분할 (Space Subdivision)
공간을 2개 이상의 겹치지 않는 (disjoin) 영역으로 나누는 것을 말한다.
보통 효율적으로 계산을 하기 위해서 공간을 나눈다.
보통 Ray Tracing, Scanline Algorithm, Collision Detecting 등에 사용된다.
공간 분할을 하는 첫 번째 방법은 View Frustrum 을 계산하는 것이다.

모델링된 공간을 실제로 화면에 다 그리는 것이 아니라
관찰자가 볼 때, 실제로 어디서부터 어디까지 보이는지 관찰가능한 영역을 잘라, 그 영역만 렌더링하는 것이다.
공간 분할하는 또 다른 방법은 BSP (Binary Space Partitioning) Tree 를 이용하는 방법이 있다.
공간을 재귀적으로 2개의 하위 공간으로 나눈 뒤, 각 하위 공간에 렌더링 순서, 가시성 계산 순서를 다르게 매겨서 이 순서에 따라 계산하고 렌더링하는 방법이다.
충돌 처리, 숨겨진 표면 제거, Ray Tracing, Robot Planning 등에 사용된다.
예를 들어 물체와 바닥의 충돌을 처리할 때는 물체의 공간을 잘게 쪼갠 뒤에 물체의 바닥 영역 공간과 실제 바닥 사이에 충돌이 일어났는지 체크하는 방식으로 계산을 단순화할 수 있을 것이다.
BSP Tree 방법의 장점은 복잡한 3D 장면에서도 효율적으로 가시성 정렬 (앞에 것이 보이고, 뒤에 것은 가려지고) 이 가능하고,
특히 정적 장면에 대해서 높은 성능을 보인다.
하지만 트리를 만드는데 시간이 오래 걸리는데다, 동적인 장면에서는 매번 트리를 재구축해야해서 성능에 좋지 않다.
따라서 이 방식은 고정된 건축 모델, 정적인 맵을 렌더링할 때 유용하다.
그 다음 방법으로는 Octree (8진트리) 를 사용한 공간 분할 기법이 있다.

이름 그대로 공간을 8개 조각으로 재귀적으로 쪼개어 표현하는 방법이다.
어느정도 충분히 쪼개졌다면 멈추고, 특정 영역에서는 더 쪼개야하면 다시 8등분으로 쪼개기를 반복하는 것이다.
이 방식은 특정 영역 데이터에 빠르게 접근할 수 있다는 장점이 있다.
(이분탐색을 응용한 알고리즘을 사용하면 로그시간에 접근 가능할 것 같다.)
따라서 충돌 감지, LoD (Level of Detail) 계산에 효과적이다.
하지만 메모리를 많이 사용하고, 데이터 분포가 불균형하면 노드도 불균형하게 만들어져 성능 향상에 방해가 되는 단점이 있다.
이 방법 역시 Ray Tracing, 충돌 감지 등에 활용될 수 있다.
Ray Tracing 에서 이 방법을 많이 사용한다고 한다.
다른 방법으로 Kd Tree (K-Demensional Tree) 가 있다.
N차원 공간을 축을 기준으로 재귀적으로 분할하는 방법이다.
Octree 가 3차원 공간을 무조건 8개 조각으로 쪼갰다면,
이 방법은 특정 축을 기준으로 쪼개므로 무조건 8개로 쪼개지는 않는다.
Ray tracing 에서 경로 추적시 더 빠르게 연산할 수 있고, 특정 좌표, 영역의 검색 속도가 빠르다는 장점이 있다.
하지만 트리의 균형을 유지하기가 어렵고, 균형이 깨지면 검색 속도가 저하되며, 동적 데이터 처리에는 적합하지 않다는 BSP Tree 와 유사한 단점을 공유한다.
마지막으로 BVH (Bounding Volume Hierachy) 방식이 있다.
물체를 감싸는 Bounding Volume (최소 경계 부피) 를 계층적으로 나누는 것이다.

예르 들어 위 포크레인의 최소 경계 부피를 구하기 위해
포크레인의 공간을 나눠서 각 공간별 경계 부피를 구하는 것과 같다.
이렇게 하면 Ray tracing 에서 광선과 객체의 교차 테스트를 효과적으로 줄일 수 있고
동적 장면에서도 효과적으로 사용할 수 있다는 장점이 있다.
하지만 초기 구축에 시간이 걸리고, 경계부피가 너무 커지면 효율성이 떨어지는 단점이 있다.
이 기법도 kd tree 와 비슷하게 ray tracing 연산 최적화를 위해 사용된다.
'CS > 컴퓨터그래픽스와 메타버스' 카테고리의 다른 글
| [그래픽스] 6. Scan Conversion (1) | 2025.06.11 |
|---|---|
| [그래픽스] 5. Rendering (3) - Lightening & Ray Tracing (0) | 2025.06.09 |
| [그래픽스] 4. Rendering (2) - Texture Mapping, Shadow Generation (1) | 2025.06.08 |
| [그래픽스] 3. Rendering (1) - Shading (0) | 2025.06.08 |
| [그래픽스] 1. 컴퓨터 그래픽스 (8) | 2025.06.07 |
