팬케이크 뒤집기 문제
어떤 무작위 수열이 존재한다.
내가 할 수 있는 연산은 수열의 prefix를 뒤집는 연산만 가능할 때,
주어진 수열을 정렬하는데 필요한 최소한의 뒤집기 연산 횟수를 구하는 문제
그리디 접근법으로 떠올릴 수 있는 제일 간단한 해결 방법 :
현재 남아있는 제일 큰 수를 맨 위로 오도록 뒤집는다 → 전체를 뒤집는다 → 제일 큰 수가 맨 밑으로 간다.
이를 반복하면 된다.


이 알고리즘은 분명 잘 작동한다.
하지만 더 적은 횟수로 문제를 풀 수는 없을까?
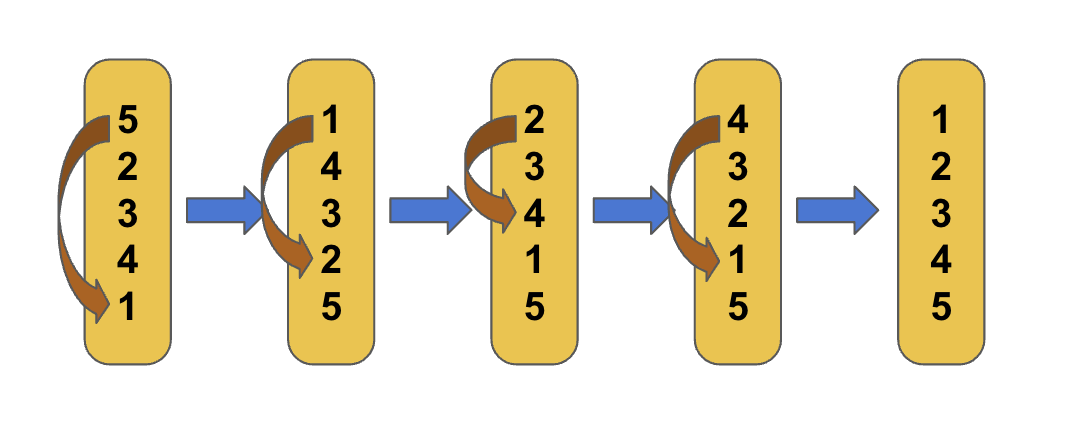
4번에 정렬할 수 있다!
사람과 쥐의 게놈은 비슷함 (여러 번의 재배치가 존재하는 차이점이 있다.)
이때 발생 가능한 재배치의 종류는 크게 4가지
1. Reversal (이번 글에서 주로 정리할 내용)
2. Fusion : 2개의 contig 가 1개로 합병
3. Fission : 1개의 contig 가 2개로 분할
4. Trnaslocation : 위치 교환 (염색체 교차를 생각하면 편하다)
Reversal
임의 영역의 순서를 뒤집는 것
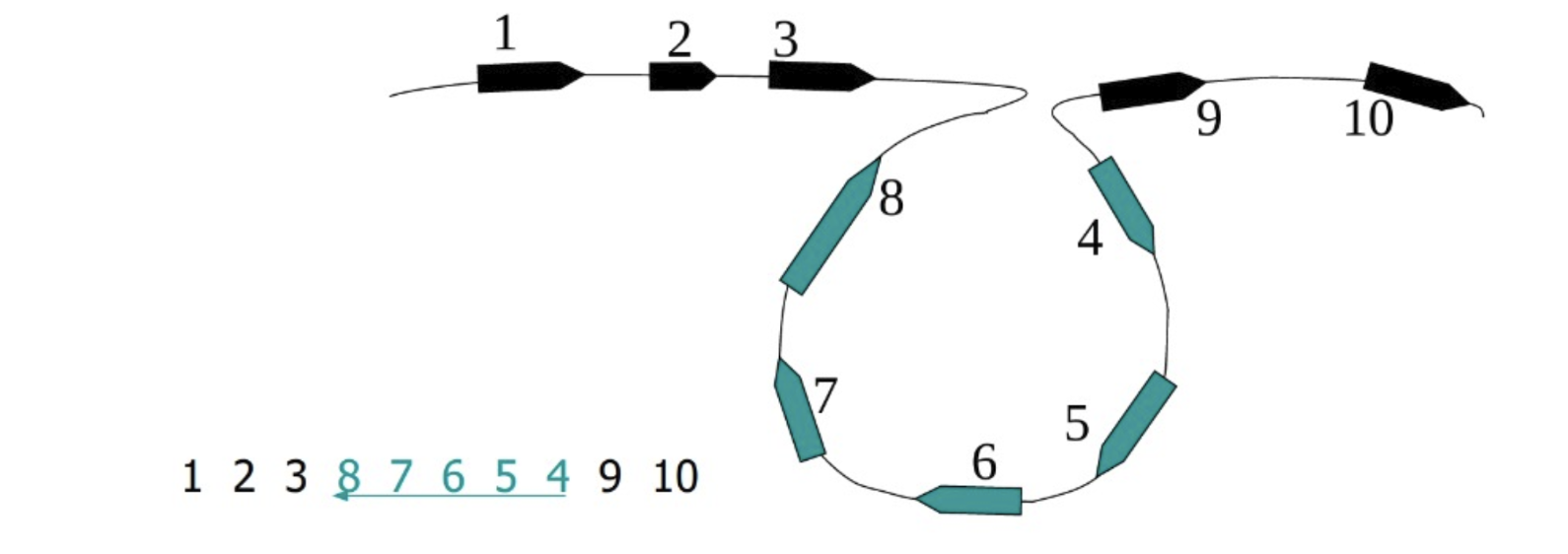
4 ~ 8 을 뒤집은 8 ~ 4 가 중간에 끼어있게 된다.
이때 뒤집으면서 순서가 안맞는 부분을 breakpoint 라고 하며, 2개의 breakpoint 가 생겨난다.

Reversal 연산은 ρ(i, j) 형태로 작성 i번째 데이터부터 j 번째 데이터 사이의 데이터를 뒤집는다는 의미
(이때 i, j 도 포함한다.)
Reversal Distance 문제
2개의 수열이 주어질 때, 하나의 수열로부터 다른 수열을 만들기 위해 필요한 최소한의 Reversal 연산 수 구하기
문제를 단순화하기 위해 destination 수열을 1~n에 매핑하고,
source 수열을 그에 매핑된 값으로 변환한다.

그러면 이런식으로 1~10 으로 정렬된 수열을 만드는 문제로 일반화된다.
위 예시는 주어진 수열을 3번의 reversal 연산으로 정렬된 수열로 만드는 방법을 보여준다.
Greedy
팬케이크 문제와 비슷하게 접근한다.
소스 수열의 앞을 봤을 때, 앞쪽이 이미 정렬되어 있을 수 있다.
그러면 reversal 범위를 잡을 때 정렬된 부분 다음에 올 숫자가 위치하도록 뒤집는다.
예를 들어서 1 2 3 7 5 ... 4 8 9 라는 수열이 있다면
왼쪽에서부터 1 2 3 은 이미 정렬되어 있다.
따라서 이제 4번째 위치에 4가 오도록 뒤집기 위해 3 다음부터 시작해서 4가 나올 때까지 만나는 모든 수열을 뒤집는 것이다.
그러면 1 2 3 4 ..... 5 7 8 9 라는 수열이 된다.

123 이 되어 있으니 4가 오도록 뒤집기
1234 가 되어 있으니 5가 오도록 뒤집기 => 끝
이 알고리즘은 최악의 경우 길이 n의 수열에 대해 n-1 번의 뒤집기를 해야할 수 있다.


위와 같은 예시를 생각해보면 greedy 알고리즘을 사용할 때 최악의 경우가 된다.
제일 간단한 방법은 1~5를 뒤집고 6 ~ 1을 뒤집는 2번의 연산이기 때문이다.
BreakPoint 활용
연속해서 증가하거나 감소하는 단위를 묶고, 묶은 단위 사이사이를 나눠준다.
그렇게 끊어지는 포인트들이 breakpoint가 된다.

1 / 9 / 3 4 / 7 8 / 2 / 6 5

b(Π) 를 breakpoint 개수로 정의한다고 한다.

이 알고리즘은 기존의 순열 앞 뒤에 0 과 n+1을 추가하는 아이디어를 사용한다.
이렇게 확장하면 break point가 늘어날 수 있다.
breakpoint 는 reversal 을 할 때 사용하는 중요한 기준점이다.
이때 우리는 '유용한 reversal' 을 정의할 수 있는데, 한번 reversal을 했을 때, 유용한 reversal 은 breakpoint 를 2개 없앤다.
또는 (사이드 쪽에서 뒤집었다면) 1개의 break 포인트를 없앨 수 있다.

위 예시를 보면 처음에 확장했을 때 5개의 b.p 가 있었지만, reversal 을 통해 1개 또는 2개씩 breakpoint 를 제거하고 있다.
breakpoint 가 없어지면 정렬이 완료된다.
이제 새롭게 strip 이라는 용어를 정의한다.
strip 은 연속하는 두 breakpoint 사이에 있는 순열을 말한다.

strip 은 크게 increasing strip / decreasing strip 으로 분류된다.

위와 같은 예시를 보자. 여러개의 strip 이 존재하는데,
제일 먼저 decreasing strip 중에서 제일 작은 원소를 갖는 strip을 선택한다.
(당연히 해당 strip은 제일 오른쪽에 있는 decreasing strip 일 것이다.)
그리고 다음으로 작은 원소를 갖는 decreasing strip 을 선택한다.
이제 두 strip 을 포함하는 reversal 구간을 잡고 뒤집는다.
위 그림 예시를 보면 처음에는 2가 포함된 strip 을 고르고, (3은 고른 스트립에 들어있으므로 빼고 생각했을 때)
다음으로 작은 값을 포함하는 감소 strip 은 4 이다.
따라서 4 ... 2 를 reversal 구간으로 잡고 뒤집는다.

기존 대비 breakpoint 가 1개 감소하였다.
다시 반복하면 이번엔 4와 7을 고른다.
따라서 8 7 .... 4 구간을 뒤집는다.
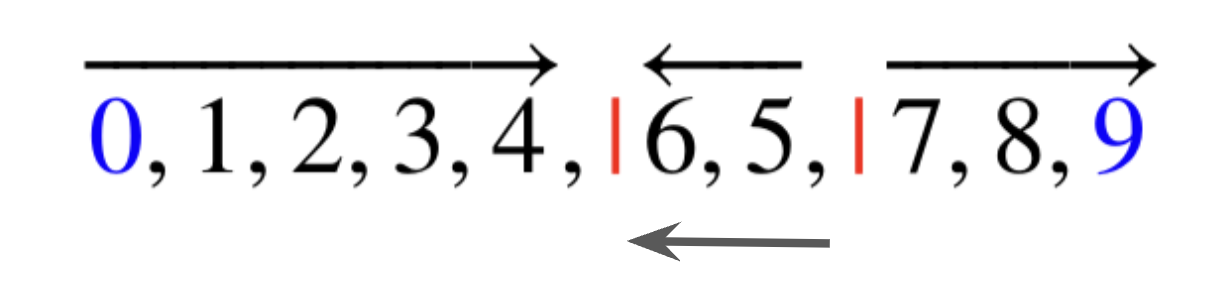
1개의 다시 감소하는 strip을 찾는다. 1개라면 그냥 뒤집는다.
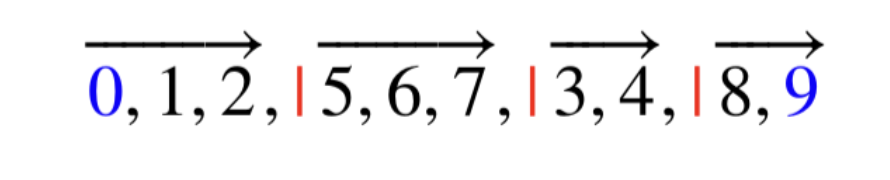
그런데 위 그림과 같이 만약 감소하는 strip이 없다면 어떻게 할 수 있을까?
아때는 임의로 뒤집어서 감소하는 strip 으로 만들면 된다.

그래서 종합하면, 증가하는 것만 있으면 임의로 잡아서 감소 스트립을 만들고,
감소 스트립과 스트립 사이를 골라서 통으로 뒤집는 과정을 통해 정렬한다.

이렇게 뒤집을 수 있다.
하지만 이 방법도 여전히 그리디하다.
'CS > 문제해결기법' 카테고리의 다른 글
| 11. Hidden Markov Models (카지노 동전 문제) (1) | 2024.12.11 |
|---|---|
| 9. 문자열 패턴 찾기 (6) | 2024.12.11 |
| 8. 단백질 서열 결정 (4) | 2024.12.10 |
| 7. Assembling a Genome (0) | 2024.10.30 |
| 6. Advanced Sequence Alignment (0) | 2024.10.29 |
