dimer (길이가 2인 k-mer) 조합은 AA 부터 CC 까지 16가지가 존재한다.
그러면 확률적으로 각각의 dimer 가 등장할 확률은 1/16으로 동일하므로, 실제 서열에서도 이와 비슷한 분포를 갖고 있어야 할 것 같다.
그런데 사람 게놈을 살펴봤더니 그렇지 않았다.
특히 CG 패턴은 매우 적었다.
이런 현상을 가리켜 CG-Island 라고 부른다.
이 문제는 The Fair Bet Casino 문제로 비유할 수 있다.
어떤 카지노 게임이 동전 던지기의 결과인 H/T 로 결과가 정해진다고 해보자.
그런데 이때 동전은 '공정한 동전 = 모두 1/2 확률' 과 '편향된 동전 = 앞면이 3/4' 이 있다.

따라서 이렇게 조건부 확률로 표현할 수 있다.
그리고 공정한 동전과 편향된 동전의 교체가 적발되면 좋지 않으므로, 코인의 교체 확률은 1/10 이라고 해보자.
이때 Fair Bet Casino 문제는 다음 문제를 푸는 것이다.
- 코인 토스의 결과 시퀀스가 주어졌을 때, 각 토스에서 어떤 동전이 사용되었는지 추측하기
사실 어떤 코인의 시퀀스라도 주어진 결과를 만들 수 있지만,
그렇다고 그 결과를 만들 확률이 동일한 것은 아니다.
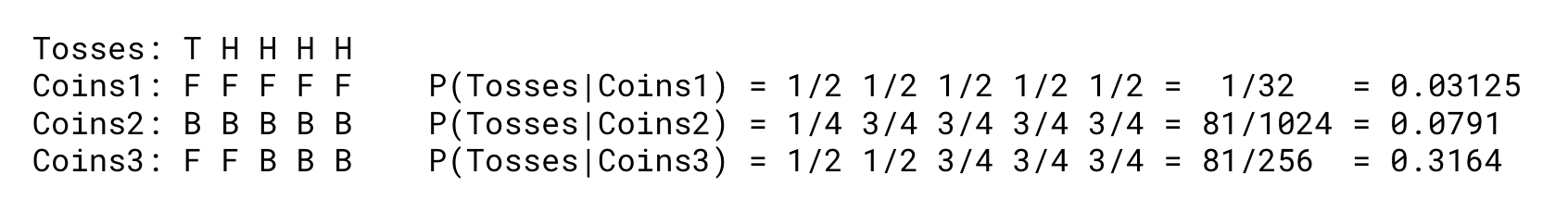
결과가 THHHH로 주어졌을 때, 공정한 코인을 5번 쓴 경우 편향된 코인을 5번 쓴 경우, 2 / 3 씩 나눠서 쓴 경우의 확률이 다르다.
그렇다면 이 문제는 어떤 코인 교체 조합이 가장 높은 확률을 갖는가? 로 대신 물어볼 수 있다.
코인 토스 결과를 signal 이라고 할 때, 가장 높은 조합의 코인 교체 조합을 찾는 것을 Decoding Problem 이라고 한다.
이 문제를 푸는 방법을 접근하기 위해 먼저 극단적인 케이스, 공정한 것만 쓰거나, 편향된 것만 쓰는 경우를 체크해보자.

각각의 확률에 대한 노테이션은 이렇게 표기한다.
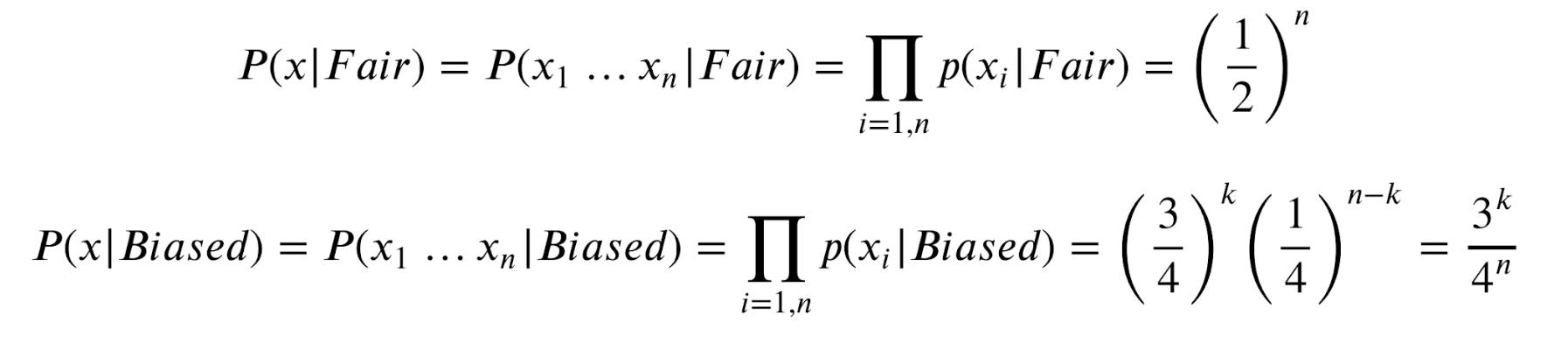
수식은 요래 나온다.
k 는 시퀀스에서 앞면이 관측된 횟수이다.
(앞 뒷면의 등장 순서도 중요하지 않나? 근데 일단 서로 다른 순서에 대해서는 같은 조합이라면 같은 확률이긴 할테니..)

그래서 이렇게 두 확률이 같은 경우를 놓고 계산해보면
k = n / log_2 3 이라서 H가 63% 이상 등장하는 경우, 편향된 코인만 썼을 확률이 증가한다.
Log Odd Ratio
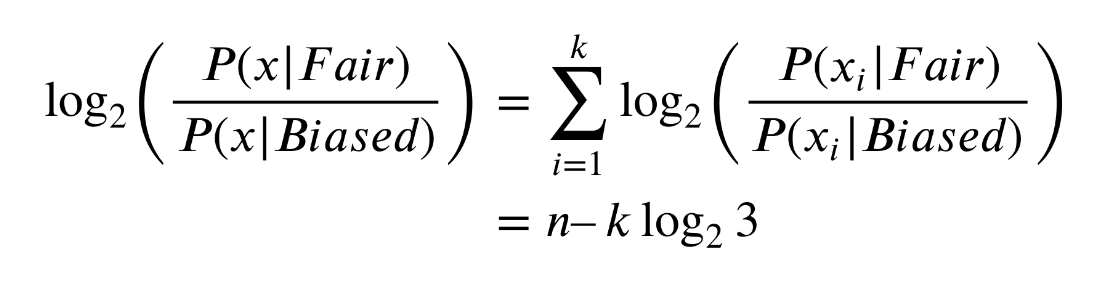
이때 새로운 개념 log-odd ratio 를 위와 같이 정의해보자.
이 개념은 '임계점' 을 나타내는 개념으로,
이 비율이 0보다 크면 공정한 코인만 썼을 확률이 높아지고 (분자)
이 비율이 0보다 작아지면 편향된 코인만 썼을 확률이 높아지고 (분모)
이 비율이 0이면 두 확률은 같다.
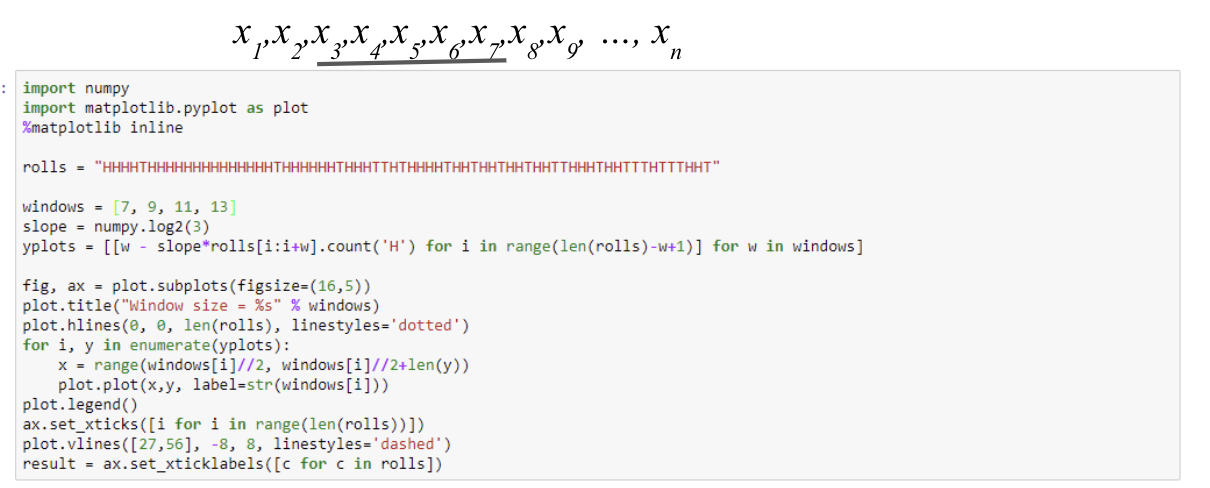
이제 어떤 HT 시퀀스가 주어질 때, 이 시퀀스를 슬라이딩 윈도우로 순회하면서 log-odd raito 를 구해보면
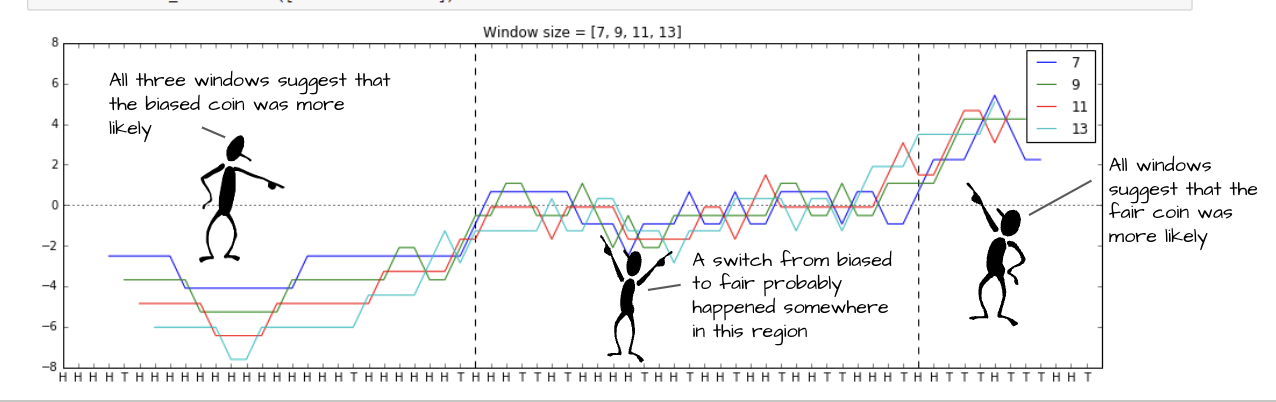
언제 공정한 코인과 편향된 코인을 교체하는지 추측할 수 있다.
윈도우 크기를 임의로 정해놓고 다 구했을 때 7, 9, 11, 13 에 대해서 모두 이때는 편향된 코인이 쓰였을 확률이 높다고 말하면 (log-odd ratio가 음수면) 거기는 편향된 코인이 쓰인거고, 상대적으로 공정한 코인이 많이 쓰였다고 말하면 (log-odd ratio가 양수면) 거기는 공정한 코인이 쓰인 것이다.
하지만 이 방법은 '윈도우 크기를 그래서 어떻게 잡는 것이 맞느냐?' 라는 것을 결정하는 것이 힘들다.
윈도우 크기마다 비슷한 영역에 대해 다르게 분류할 수 있기 때문이다.
HMM
이 문제를 한번 다르게 모델링해서 풀어보자.

먼저 기존에는 조건부 확률로 표시햇떤 것을 아래와 같이 나타낸다.
코인과 코인의 transition 조합을 전제로 한 확률을 구해보는 것이다.
문제에서 코인이 바뀔 확률은 1/10 이라고 하였으므로,
2개의 연속한 결과에 대해서
B → B 를 썼을 확률은 0.9
F → B 를 썼을 확률은 0.1
B → F 를 썼을 확률은 0.1
F → F 를 썼을 확률은 0.9
이런 상태 변화의 확률을 '숨겨진 상태' 라고 말하고, 이 '숨겨진 상태'에 기반해서 확률을 계산해보는 것이 HMM 이다.
(Hidden Markov Models)
이런 카지노 문제와 비슷한 유형의 문제를 푸는 방식으로, 알파벳 심볼을 출력으로 내는 Hidden State 를 k개 가진 추상화된 기계로 문제를 모델링한다. (오토마타 생각이 난다)
각 동작마다 이 기계는 2가지를 결정해야 한다.
1. 현재 상태에서 어떤 결과를 낼 것인가
2. 다음에 상태를 바꿀 것인가 유지할 것인가

웃자고 넣으신 예시인데 생각보다 좋은 예시같다.
교수님의 기분이 좋은 상태 / 나쁜 상태 일 때의 따라 연습문제를 풀지, 명확하게 설명할지, 수업을 일찍 끝낼지 확률이 달라진다고 할 때 이를 이렇게 그림으로 표현한 것이다.
(간선을 보면 기분이 나쁠 때 계속 나쁠 확률은 0.9 인데, 기분이 좋을 때 계속 좋을 확률은 0.6이다...)
이제 이 문제는 output (위 예시에서는 교수님의 행동) 이 주어졌을 때, 이를 도출할 확률이 가장 높은 hidden state 서열을 찾는 문제로 바뀐다.

동전 문제는 이렇게 상태 기계로 표현할 수 있다. (오토마타 관점에서 보면 NFA와 유사하다)
숨겨진 상태는 네모로 표시하고, 출력하는 심볼은 동그라미 상태로 표시한다.

이제 원래의 카지노 문제를 풀어보자.

주어진 path 의 확률은 이렇게 구한다.
i번째 숨겨진 상태가 π 일 때의 그 결과 x가 나올 확률과 현재 상태에서 상태가 변경될 확률을 곱한 것을 모든 i 에 대해 곱한다.
이때 가능한 path 의 가짓수는 숨겨진 상태가 2개이므로 2ⁿ 이다.
그러면 가장 높은 확률을 찾기 위해 모든 패스를 다 해봐야만 하는 걸까
브루트 포스는 너무 오래걸리는 것이 자명하고, 패스를 임의로 둘로 쪼개서 각각 계산하는, DP도 생각할 수 있는데,
강의록에서는 맨하튼 그래프로 모델링 하는 방법을 소개한다.
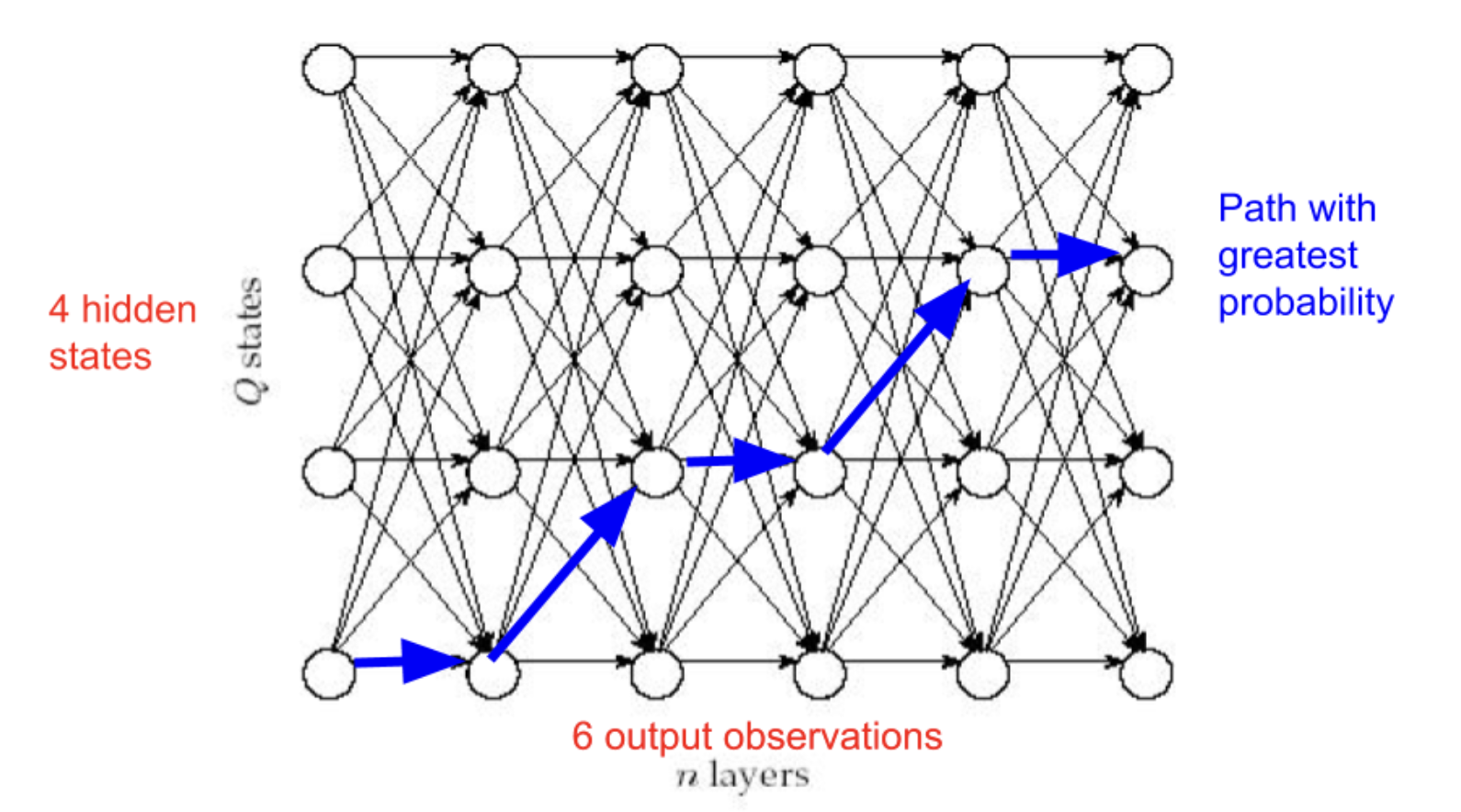
위 그림은 4개의 숨겨진 상태가 있고, 6개의 결과가 주어질 때 최적의 경로를 찾는 문제로 생각할 수 있다.
그러면 우리가 찾는 결과는 최적의 결과에 대해 hidden states 의 시퀀스만 답으로 취하면 된다.

이를 카지노 문제에 적용하면 요래된다.
DP를 이용하면 각 레이어의 확률을 구해두고 그 값을 기반으로 다음 레이어의 확률을 쉽게 구할 수 있으므로 탐색 영역의 크기를 줄일 수 있다.
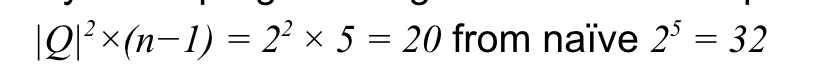
왜인지는 모르겠으나, (숨겨진 상태의 가짓수 제곱) x (주어진 결과 시퀀스의 길이 -1 ) 를 하면 된다고 한다.
그리고 이렇게 그래프로 표현한 문제를 푸는 것은 마치 DAG 에서 최'장'경로를 구하는 것과 같다.
(DAG = 사이클이 없는 방향 그래프)
Viterbi Decoding Algorithm

그런데 확률 계산은 곱셈이니까 원본 데이터에 로그를 취하면 곱셈 말고 덧셈으로 구할 수 있다. (맞나?)
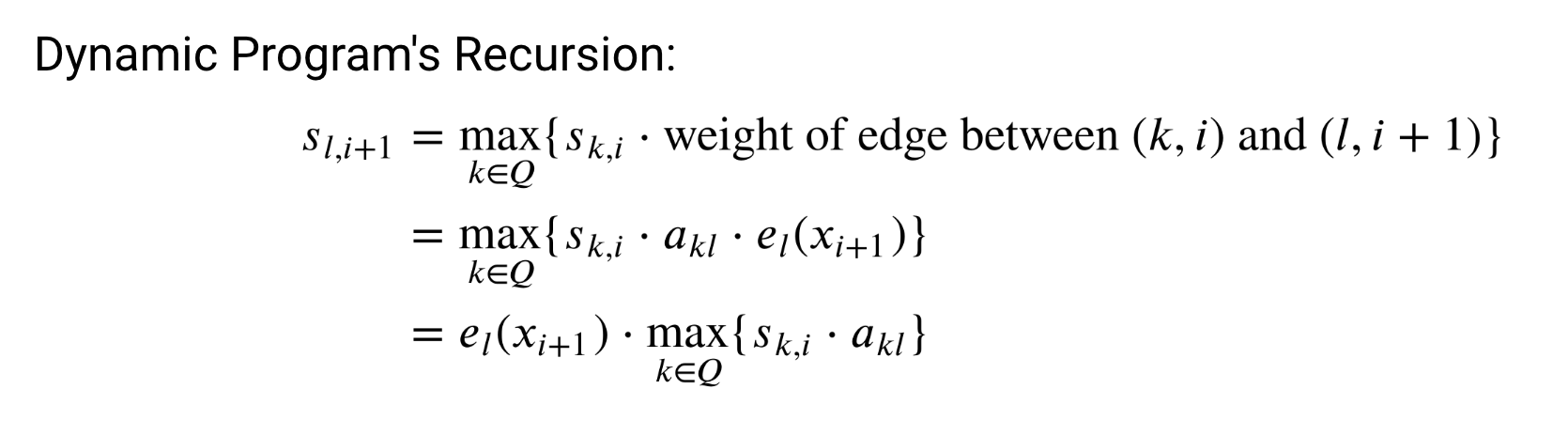
그리고 위 항은 DP 점화식을 통해 이렇게 구할 수 있다.

계산해보면 0.005 와 0.006 이 나오며, 제일 큰 값은 0.006 이고, 이 값이 계산된 경로는 계속 B를 고른 경우라서
제일 확률이 높은 코인 조합은 BBBBBB 라고 한다.

그런데 FFFFFF도 거의 비슷한 확률을 갖고 있는데, 결과값이 조금 더 높다는 이유로 확정지을 수 있을까?
(라는 문제가 있는 것 같다)


마지막으로.. 카지노 문제로 돌아와서 HMM이 도출한 솔루션과 비슷한 결과를 내는 다른 솔루션이 존재하는지 판단하는 문제를 생각해보면
이를 Forward-Backward Problem 이라고 한다.
이 문제는 HMM으로 구한 hidden state 시퀀스가 주어졌을 때, 특정 flip 에서 사용되었을 확률이 가장 높은 동전을 찾는 것이다.
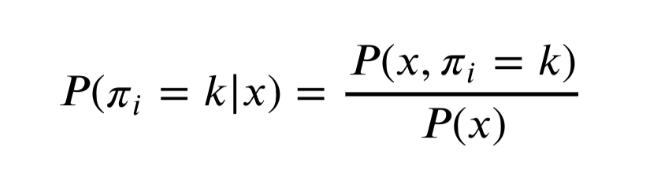
확률은 이렇게 구할 수 있나보다
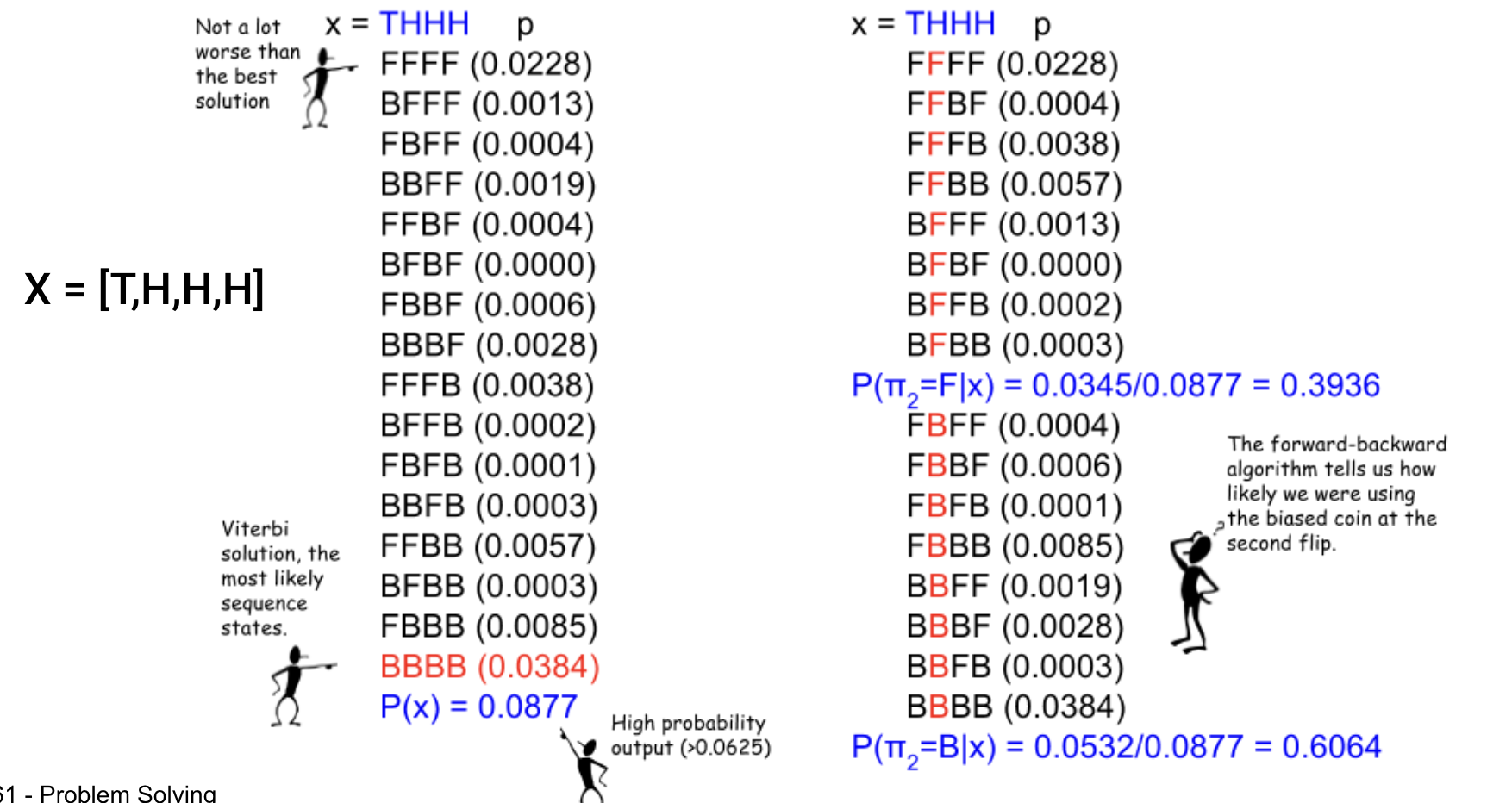
왼쪽 그림은 THHH를 도출하는 가장 높은 확률을 갖는 동전 사용 조합을 찾는 HMM을 보여주고
오른쪽 그림은 THHH 에서 H 시점에 어떤 동전이 사용되었을 확률이 가장 높은지 찾는 문제이다.
Forward 알고리즘에서는 이렇게 구한다.

f_k,i 의 정의는 1부터 i 까지 x1, x2 , .... , x_i 의 코인 토스 결과 prefix 를 만들었고, 마지막 상태가 k 일 확률을 말한다.
기존의 viterbi 알고리즘과 유사할 수 밖에 없는 건, 기존 문제를 i까지로 축소하고 풀면 되기 때문
하지만 구하려는 확률 (전체 토스 결과 시퀀스가 주어질 때, 특정 위치에서 어떤 동전이 사용되었을 확률이 제일 높은지) 을 얻기 위해서는 forward 알고리즘 말고 backward 알고리즘도 필요하다.

그건 이렇게 구한다고 한다.
i 위치에서의 확률을 구할 때, i → i+1 로 상태가 어떻게 변화하는지, 어떤 결과를 내는지에 따라서도 값이 달라질 수 있기 때문이다.
backward 에서 구하는 확률은 i번째에 k라는 히든 상태에 있을 때, 그 뒤로 i+1 ~ n 까지의 토스 결과를 도출할 확률이다.

그래서 최종적으로는 요래 구하면 된다고 한다.

위는 구하는 예시
'CS > 문제해결기법' 카테고리의 다른 글
| 10. 게놈 재배치 (팬케이크 뒤집기 문제) (0) | 2024.12.11 |
|---|---|
| 9. 문자열 패턴 찾기 (6) | 2024.12.11 |
| 8. 단백질 서열 결정 (4) | 2024.12.10 |
| 7. Assembling a Genome (0) | 2024.10.30 |
| 6. Advanced Sequence Alignment (0) | 2024.10.29 |
